Load and power generation management are important tasks in the operation of power systems. Due to its complexity, we have broken down the planning problem into several planning stages for hierarchical organizations with different time horizons and goals. For the short-term operation plan, it has a planning period of one day to several days, with a time step of 15 minutes. Its purpose is to minimize the cost of a particular demand energy production or to maximize the profit of a particular energy price. Even with smaller power systems, the planning problems that arise are very complicated. Therefore, computer-based application software is required to support the operation of such systems.
Operators of thermoelectric systems or water-thermoelectric systems plan long-term operations to determine their own power generation and the availability of other available energy sources, such as purchasing energy in the form of contracts. The purpose of the plan is to minimize the operating costs of the power system or maximize profits. For this reason, operators must consider a large number of technologies, contracts, and environmental and government restrictions. In addition, the user's load over time must be taken into account.
If it is necessary to provide users with several types of energy, operational planning problems can become particularly difficult. In particular, the following features of this type of multi-energy system increase the need for optimization:
1) The load characteristics of different loads over time, such as electricity (peak at noon) and district heating (peak in the morning) are different. Therefore, the load model in the optimization period must consider the concurrency of the load.
2) Multi-energy generating units, such as cogeneration units, have a correlation between electricity production and heating.
3) On the other hand, different characteristics of energy sources limit the scope of the operation plan. The operating plan can use the ability to store energy (water, gas, or heat) that allows the genset to have different uses.
Due to its complexity, we subdivide the planning problem into the planning stages of several hierarchical organizations, which have different time periods and goals. The result of the upper stage is the input of the lower stage. In short, the three-division plan issue will be of great help to the work, as shown in Figure 1.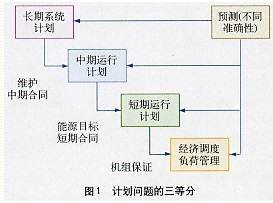
The medium-term operation plan is the first part, and the optimization period is from weeks to 15 months. Usually called the annual plan. The central task of this section is to determine the target amount of primary and secondary energy in the entire time range and part of the time range. Including the storage management of large reservoirs and the management of long-term contracts.
The short-term operation plan includes a time range from one day to one week, with a time step of 15 minutes. Since the scope of the plan is in the near future, a higher quality load forecast than in the medium-term operation plan can be used. Its purpose is to determine the optimal progress of the generator set and the energy contract under all relevant constraints.
Last but not least, the ultra-short-term operation plan calculates all the economic load schedules that determine the generator set and all flexible loads.
Due to the liberalization of energy markets, the importance of short-term contracts and trade is increasing. Often contractual conditions are established, such as the limitations of an actual power plant, so that the supplier's energy flow system and its additional complexity increase with the number of contracts. Therefore, computer-assisted short-term operation plans have become increasingly important.
Although the generalized optimization model classifies the planning problem, even for smaller power systems, the final optimization task is still difficult to solve. Power companies often use computer-based planning packages to support operators. These packages use mathematical algorithms to determine the best solution for the planning department. This requires converting the original actual plan problem into a mathematical formula. The process is called modelling. This conversion step presents challenges for the development and execution of such software packages. In many countries, power companies have been in transition for several reasons. First, many countries have liberalized energy markets. This has led to new business opportunities, new energy contracts or energy trade. This means that the plan must take into account the new contractual requirements modeled in the optimization package. Second, climate protection has become more and more important. Therefore, new generator sets will be installed and the power system must take into account new environmental restrictions. Finally, power companies must perform scenario analysis to adapt the system to increasing energy consumption.
If the modeling of the optimization package is not flexible and cannot adapt to new needs, its calculation results will become worthless. This is the main reason why operators do not adopt such systems even if they do not doubt the general advantages of mathematical optimization.
To this end, modeling of actual optimization problems plays a key role in the development and execution of operational planning packages: on the one hand, the main part of the planning problem must be covered with great flexibility; on the other hand, it must be easy to use so that operators can Use an optimization model and stay up-to-date. Therefore, it must be determined which part of the power system is relevant to the operation plan. Based on such specifications, generalized basic objects can be developed to provide a mathematical description of the components of the power system.
Figure 2 depicts a generalized energy model of a multi-energy system with the most important components. Basic generalized objects can be found in almost every system. They contain three basic goals: process goals, balance, and storage. In addition, the three auxiliary objects of time limit, time series, and function axis describe the details of the basic target.
The process object describes the determined input and output relationship components. The functional correlation between one or more input and output values ​​is expressed by a mathematical equation (characteristic curve). The operating range of a process object may depend on other process objects, such as the extraction of a modeled condensing steam turbine. Examples of basic process objects are heat transformers, hydrodynamic converters, lines or contracts.
The feasibility of a process object can be influenced by additional constraints and cost factors. They are valid throughout the planning period or sub-planning period. For example, the availability of components, power and energy limits or minimum operating and downtime all fall under these additional constraints.
Model object balance concentrates, accumulates, and limits the power or energy of a given process according to the time network. These balances are related to a certain energy source and are also related to different amounts, such as emissions or auxiliary medium consumption like cooling water.
Using these basic model objects, macroscopic objects can be established to model more complex power system components, such as cogeneration units with waste heat boilers. In addition, this flexible modelling will also consider new situations where basic model objects are used in different scopes. Two examples illustrate this situation.
In the first example, power system operators want to examine whether it is profitable to purchase or sell electricity in energy trading. Energy trading offers three different products one day ahead of schedule. Basic products, non-peak load products and peak load products (see Figure 3).
For the mathematical formula of the optimization problem, it means that the general energy model must be extended by reflecting the process object of the contract. They must increase in two aspects: first, sell energy to the trading market, and first, purchase energy from the trading market (see Figure 4).
After optimization, the solution is shown in Figure 5. In other words, the power system should sell peak-load products to the trading market, and purchase non-peak-load products from the energy trading market. Base load products should not be used.
The second example relates to the Kyoto Protocol. Within the EU, the collapsed country promised to reduce carbon dioxide emissions. To this end, member states have established a certificate system. Large users of carbon dioxide emissions must purchase these emission certificates. In other words, carbon dioxide emissions must be considered in the operating plan. For this reason, the model object of the thermo-generator set in Fig. 2 is related to the new equilibrium object of carbon dioxide emission. This balance is related to the contract object that represents the certificate and its cost.
Both examples clearly illustrate the advantages of the generalized model components. Unlike the examples, such as trade in the trading market and carbon dioxide considerations, the standard basic model object can be used to establish a mathematical optimization model. To this end, power system operators can adapt mathematics optimization to changing requirements. Therefore, the advantages of the software package remain unchanged.
The generalized optimization model of the month is optimized by XOPT To achieve the advantages of the generalized optimization model, the optimization package XOPT is developed. The tree menu of the XOPT user interface is shown in FIG. 6 . It provides a high degree of flexibility in modelling in order to adapt to various tasks in the optimal operation of the energy system.
l. XOPT user interface Modeling with XOPT also means choosing objects from a small set of modules. The abstract targets are parameterized and these objects become models of the actual structure. In other words, operators can change and adjust their energy flow models at any time through the user interface. He can combine new components or remove objects that are no longer important.
The user interface is based on the well-known MSExcel, which allows the use of Excel's features to create specific input tables and/or result tables and link them to the subject XOPT data.
Figure 7 shows the input table for a typical energy flow model.
2. The large input of XOPT input/output planning tasks can be divided into three categories: The first type is the model topology, which components of the energy flow model are composed of and how these components interact. In addition, major data such as characteristic curves or absolute technical limits belong to this group. The second group consists of forecast data. According to the components of the energy system and the optimization problems to be solved, a large number of loads, prices, and/or flows are pre-loaded. The third category is dynamic operating data. The current unit status, current reserve levels, current unit availability, temporary limits, and other conditions are described here.
The results include the target value and a list of modeled parts. That is to say, for each step within the scope of the plan, the power generation per power plant, the level of each reserve, the execution of each contract, the crew guarantee, and other content are provided. In addition, the marginal cost of each balancing is calculated. In addition to the forms, the results are described graphically and summarized in the standard report.
3. The input and output classification of XOPT core program XOPT core program is shown in Figure 8.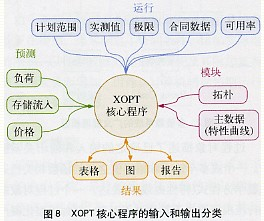
The input to the user interface provides data to the XOPT core program. The XOPT core program is based on the business software GAMS (Generalized Algebraic Modeling System) to formulate the mathematical model (variables, equations, parameters) of the basic module.
Process objects mathematically reflect various variables, while balanced objects reflect all equations. Storage objects are a mixture of the two. The algebraic equations of the basic module are of the linear type, which means that the digital model leads to linear programming problems. In order to also be able to model the nonlinear relationship, a piecewise linear characteristic curve is established. The number of steps (discretization) can be selected variables so that the approximate deviation can be sufficiently reduced. Type-binary additional variables allow modelling of decision variables, and eventually we get the category-mixed integer linear programming mathematical model (MILP). Depending on the number of energy system components and the length of the time frame, the size of the model can lead to thousands of variables and equations.
This type of problem can be solved by various commercial solvers. XOPT supports child solvers (such as CPLEX, OSL, XPRESS, etc.) through the GAMS interface.
The advantage of this concept is the use of a powerful mature algebra model language. The model and solver are separate, allowing the current best-fit algorithm to be used.
Examples using XOPT Two examples of practical application of XOPT are provided below, which reflect the flexibility in handling different optimization tasks.
1. Cogeneration and contract management of municipal utilities For municipal utilities, the energy flow model consists of several cogeneration systems, hydropower plants, bilateral contracts, and trading products. Primary energy sources are natural gas and crude oil.
The purpose of the optimization task is to calculate the most profitable schedule and the most flexible contract for the power plant to meet the electricity and heating needs of the user. Of course, the relevant restrictions must be considered. The time range is one week in advance.
Figures 9 and 10 show the best electricity and district heating distribution results for the existing units.
2. Natural gas reserve management for German gas suppliers In a German municipal natural gas utility, the XOPT package is used for natural gas reserve management. The company purchases natural gas from external suppliers and then distributes it to retail customers through the local gas supply network. The contract stipulates the external supplier's supply restrictions, and the most relevant aspect of the cost is the maximum annual air supply. Therefore, the mission of XOPT is to calculate the plan for running the facility so as to meet the user's needs and use it to maintain a low maximum hourly air supply. Operational facilities include the management of natural gas reserve load dumps.
Figure 11 shows the plan for natural gas reserve control.
Conclusion This paper demonstrates the importance of planning problem modeling for successful use of such software packages. By using a generalized basic model, the optimization model can be adapted to changing requirements, and the advantages of the software can also be preserved.
Operators of thermoelectric systems or water-thermoelectric systems plan long-term operations to determine their own power generation and the availability of other available energy sources, such as purchasing energy in the form of contracts. The purpose of the plan is to minimize the operating costs of the power system or maximize profits. For this reason, operators must consider a large number of technologies, contracts, and environmental and government restrictions. In addition, the user's load over time must be taken into account.
If it is necessary to provide users with several types of energy, operational planning problems can become particularly difficult. In particular, the following features of this type of multi-energy system increase the need for optimization:
1) The load characteristics of different loads over time, such as electricity (peak at noon) and district heating (peak in the morning) are different. Therefore, the load model in the optimization period must consider the concurrency of the load.
2) Multi-energy generating units, such as cogeneration units, have a correlation between electricity production and heating.
3) On the other hand, different characteristics of energy sources limit the scope of the operation plan. The operating plan can use the ability to store energy (water, gas, or heat) that allows the genset to have different uses.
Due to its complexity, we subdivide the planning problem into the planning stages of several hierarchical organizations, which have different time periods and goals. The result of the upper stage is the input of the lower stage. In short, the three-division plan issue will be of great help to the work, as shown in Figure 1.
The short-term operation plan includes a time range from one day to one week, with a time step of 15 minutes. Since the scope of the plan is in the near future, a higher quality load forecast than in the medium-term operation plan can be used. Its purpose is to determine the optimal progress of the generator set and the energy contract under all relevant constraints.
Last but not least, the ultra-short-term operation plan calculates all the economic load schedules that determine the generator set and all flexible loads.
Due to the liberalization of energy markets, the importance of short-term contracts and trade is increasing. Often contractual conditions are established, such as the limitations of an actual power plant, so that the supplier's energy flow system and its additional complexity increase with the number of contracts. Therefore, computer-assisted short-term operation plans have become increasingly important.
Although the generalized optimization model classifies the planning problem, even for smaller power systems, the final optimization task is still difficult to solve. Power companies often use computer-based planning packages to support operators. These packages use mathematical algorithms to determine the best solution for the planning department. This requires converting the original actual plan problem into a mathematical formula. The process is called modelling. This conversion step presents challenges for the development and execution of such software packages. In many countries, power companies have been in transition for several reasons. First, many countries have liberalized energy markets. This has led to new business opportunities, new energy contracts or energy trade. This means that the plan must take into account the new contractual requirements modeled in the optimization package. Second, climate protection has become more and more important. Therefore, new generator sets will be installed and the power system must take into account new environmental restrictions. Finally, power companies must perform scenario analysis to adapt the system to increasing energy consumption.
If the modeling of the optimization package is not flexible and cannot adapt to new needs, its calculation results will become worthless. This is the main reason why operators do not adopt such systems even if they do not doubt the general advantages of mathematical optimization.
To this end, modeling of actual optimization problems plays a key role in the development and execution of operational planning packages: on the one hand, the main part of the planning problem must be covered with great flexibility; on the other hand, it must be easy to use so that operators can Use an optimization model and stay up-to-date. Therefore, it must be determined which part of the power system is relevant to the operation plan. Based on such specifications, generalized basic objects can be developed to provide a mathematical description of the components of the power system.
Figure 2 depicts a generalized energy model of a multi-energy system with the most important components. Basic generalized objects can be found in almost every system. They contain three basic goals: process goals, balance, and storage. In addition, the three auxiliary objects of time limit, time series, and function axis describe the details of the basic target.
The feasibility of a process object can be influenced by additional constraints and cost factors. They are valid throughout the planning period or sub-planning period. For example, the availability of components, power and energy limits or minimum operating and downtime all fall under these additional constraints.
Model object balance concentrates, accumulates, and limits the power or energy of a given process according to the time network. These balances are related to a certain energy source and are also related to different amounts, such as emissions or auxiliary medium consumption like cooling water.
Using these basic model objects, macroscopic objects can be established to model more complex power system components, such as cogeneration units with waste heat boilers. In addition, this flexible modelling will also consider new situations where basic model objects are used in different scopes. Two examples illustrate this situation.
In the first example, power system operators want to examine whether it is profitable to purchase or sell electricity in energy trading. Energy trading offers three different products one day ahead of schedule. Basic products, non-peak load products and peak load products (see Figure 3).
For the mathematical formula of the optimization problem, it means that the general energy model must be extended by reflecting the process object of the contract. They must increase in two aspects: first, sell energy to the trading market, and first, purchase energy from the trading market (see Figure 4).
After optimization, the solution is shown in Figure 5. In other words, the power system should sell peak-load products to the trading market, and purchase non-peak-load products from the energy trading market. Base load products should not be used.
The second example relates to the Kyoto Protocol. Within the EU, the collapsed country promised to reduce carbon dioxide emissions. To this end, member states have established a certificate system. Large users of carbon dioxide emissions must purchase these emission certificates. In other words, carbon dioxide emissions must be considered in the operating plan. For this reason, the model object of the thermo-generator set in Fig. 2 is related to the new equilibrium object of carbon dioxide emission. This balance is related to the contract object that represents the certificate and its cost.
Both examples clearly illustrate the advantages of the generalized model components. Unlike the examples, such as trade in the trading market and carbon dioxide considerations, the standard basic model object can be used to establish a mathematical optimization model. To this end, power system operators can adapt mathematics optimization to changing requirements. Therefore, the advantages of the software package remain unchanged.
The generalized optimization model of the month is optimized by XOPT To achieve the advantages of the generalized optimization model, the optimization package XOPT is developed. The tree menu of the XOPT user interface is shown in FIG. 6 . It provides a high degree of flexibility in modelling in order to adapt to various tasks in the optimal operation of the energy system.
l. XOPT user interface Modeling with XOPT also means choosing objects from a small set of modules. The abstract targets are parameterized and these objects become models of the actual structure. In other words, operators can change and adjust their energy flow models at any time through the user interface. He can combine new components or remove objects that are no longer important.
The user interface is based on the well-known MSExcel, which allows the use of Excel's features to create specific input tables and/or result tables and link them to the subject XOPT data.
Figure 7 shows the input table for a typical energy flow model.
2. The large input of XOPT input/output planning tasks can be divided into three categories: The first type is the model topology, which components of the energy flow model are composed of and how these components interact. In addition, major data such as characteristic curves or absolute technical limits belong to this group. The second group consists of forecast data. According to the components of the energy system and the optimization problems to be solved, a large number of loads, prices, and/or flows are pre-loaded. The third category is dynamic operating data. The current unit status, current reserve levels, current unit availability, temporary limits, and other conditions are described here.
The results include the target value and a list of modeled parts. That is to say, for each step within the scope of the plan, the power generation per power plant, the level of each reserve, the execution of each contract, the crew guarantee, and other content are provided. In addition, the marginal cost of each balancing is calculated. In addition to the forms, the results are described graphically and summarized in the standard report.
3. The input and output classification of XOPT core program XOPT core program is shown in Figure 8.
Process objects mathematically reflect various variables, while balanced objects reflect all equations. Storage objects are a mixture of the two. The algebraic equations of the basic module are of the linear type, which means that the digital model leads to linear programming problems. In order to also be able to model the nonlinear relationship, a piecewise linear characteristic curve is established. The number of steps (discretization) can be selected variables so that the approximate deviation can be sufficiently reduced. Type-binary additional variables allow modelling of decision variables, and eventually we get the category-mixed integer linear programming mathematical model (MILP). Depending on the number of energy system components and the length of the time frame, the size of the model can lead to thousands of variables and equations.
This type of problem can be solved by various commercial solvers. XOPT supports child solvers (such as CPLEX, OSL, XPRESS, etc.) through the GAMS interface.
The advantage of this concept is the use of a powerful mature algebra model language. The model and solver are separate, allowing the current best-fit algorithm to be used.
Examples using XOPT Two examples of practical application of XOPT are provided below, which reflect the flexibility in handling different optimization tasks.
1. Cogeneration and contract management of municipal utilities For municipal utilities, the energy flow model consists of several cogeneration systems, hydropower plants, bilateral contracts, and trading products. Primary energy sources are natural gas and crude oil.
The purpose of the optimization task is to calculate the most profitable schedule and the most flexible contract for the power plant to meet the electricity and heating needs of the user. Of course, the relevant restrictions must be considered. The time range is one week in advance.
Figures 9 and 10 show the best electricity and district heating distribution results for the existing units.
2. Natural gas reserve management for German gas suppliers In a German municipal natural gas utility, the XOPT package is used for natural gas reserve management. The company purchases natural gas from external suppliers and then distributes it to retail customers through the local gas supply network. The contract stipulates the external supplier's supply restrictions, and the most relevant aspect of the cost is the maximum annual air supply. Therefore, the mission of XOPT is to calculate the plan for running the facility so as to meet the user's needs and use it to maintain a low maximum hourly air supply. Operational facilities include the management of natural gas reserve load dumps.
Figure 11 shows the plan for natural gas reserve control.
Conclusion This paper demonstrates the importance of planning problem modeling for successful use of such software packages. By using a generalized basic model, the optimization model can be adapted to changing requirements, and the advantages of the software can also be preserved.
Polycarbonate Solid Sheet ,Solid Polycarbonate Roofing Sheets,Clear Solid Polycarbonate Sheet,4Mm Solid Polycarbonate Sheet
NINGBO CHAOMEI PLASTIC CO.,LTD , https://www.pcban88.com